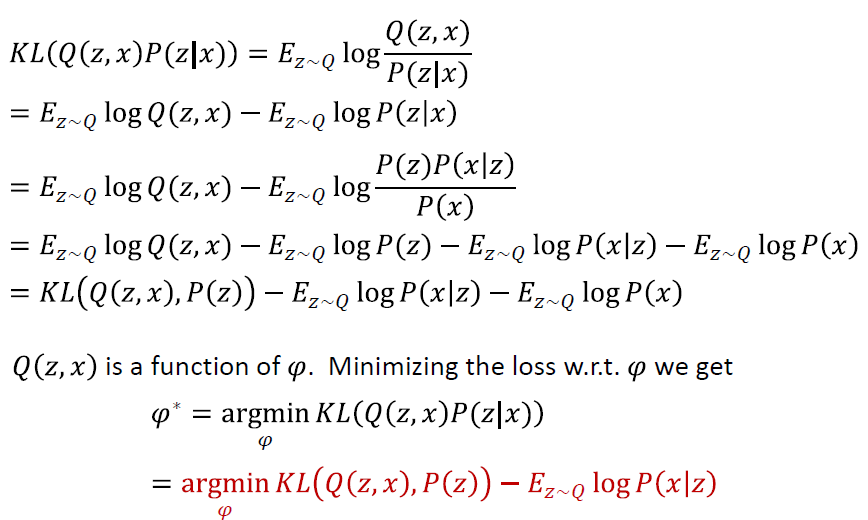Non-linear extensions of linear Gaussian models.

EM for PCA

With complete information

• If we knew $z$ for each $x$, estimating $A$ and $D$ would be simple

$x=A z+E$

$P(x \mid z)=N(A z, D)$

• Given complete information $\left(x_{1}, z_{1}\right),\left(x_{2}, z_{2}\right)$

$\underset{A, D}{\operatorname{argmax}} \sum_{(x, z)} \log P(x, z)=\underset{A, D}{\operatorname{argmax}} \sum_{(x, z)} \log P(x \mid z)$

$=\underset{A, D}{\operatorname{argmax}} \sum_{(x, Z)} \log \frac{1}{\sqrt{(2 \pi)^{d}|D|}} \exp \left(-0.5(x-A z)^{T} D^{-1}(x-A z)\right)$

• We can get a close form solution: $A = XZ^{+}$
• But we don't have $Z$ => missing

With incomplete information

• Initialize the plane
• Complete the data by computing the appropriate $z$ for the plane
  • $P(z|X;A)$ is a delta, because $E$ is orthogonal to $A$
• Reestimate the plane using the $z$
• Iterate

Linear Gaussian Model

• PCA assumes the noise is always orthogonal to the data
  • Not always true
• The noise added to the output of the encoder can lie in any direction (uncorrelated)
• We want a generative model: to generate any point
  • Take a Gaussian step on the hyperplane
  • Add full-rank Gaussian uncorrelated noise that is independent of the position on the hyperplane
    • Uncorrelated: diagonal covariance matrix
    • Direction of noise is unconstrained

With complete information

$x=A z+e$

$P(x \mid z)=N(A z, D)$

• Given complete information $X=\left[x_{1}, x_{2}, \ldots\right], Z=\left[z_{1}, z_{2}, \ldots\right]$

$\underset{A, D}{\operatorname{argmax}} \sum_{(x, z)} \log P(x, z)=\underset{A, D}{\operatorname{argmax}} \sum_{(x, z)} \log P(x \mid z)$

$=\underset{A, D}{\operatorname{argmax}} \sum_{(x, z)} \log \frac{1}{\sqrt{(2 \pi)^{d}|D|}} \exp \left(-0.5(x-A z)^{T} D^{-1}(x-A z)\right)$

$=\underset{A, D}{\operatorname{argmax}} \sum_{(x, z)}-\frac{1}{2} \log |D|-0.5(x-A z)^{T} D^{-1}(x-A z)$

• We can also get closed form solution

With incomplete information

Option 1

• In every possible way proportional to $P(z|x)$ (Gaussian)
• Compute the solution from the completed data

$\underset{A, D}{\operatorname{argmax}} \sum_{x} \int_{-\infty}^{\infty} p(z \mid x)\left(-\frac{1}{2} \log |D|-0.5(x-A z)^{T} D^{-1}(x-A z)\right) d z$

• The same as before

Option 2

• By drawing samples from $P(z|x)$
• Compute the solution from the completed data

The intuition behind Linear Gaussian Model

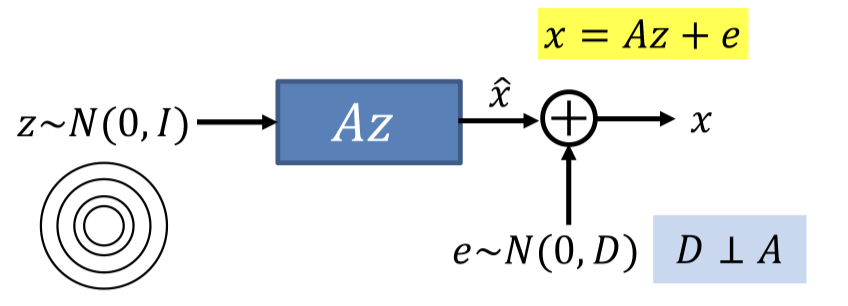
• $z \sim N(0, I)$ => $Az$
  • The linear transform stretches and rotates the K-dimensional input space onto a Kdimensional hyperplane in the data space
• $X = Az +E$
  • Add Gaussian noise to produce points that aren’t necessarily on the plane

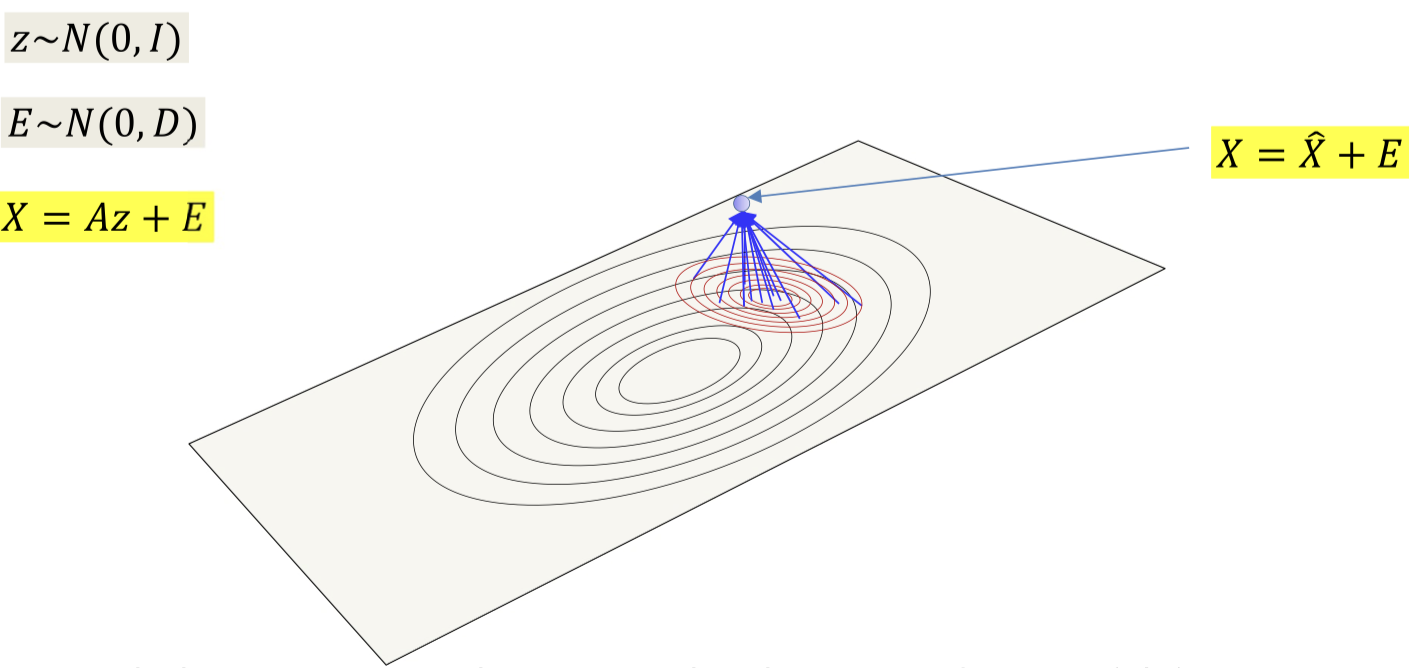
• The posterior probability $P(z|x)$ gives you the location of all the points on the plane that could have generated $x$ and their probabilities

• What about data that are not Gaussian distributed close to a plane?

  • Linear Gaussian Models fail
• How to do that

Non-linear Gaussian Model

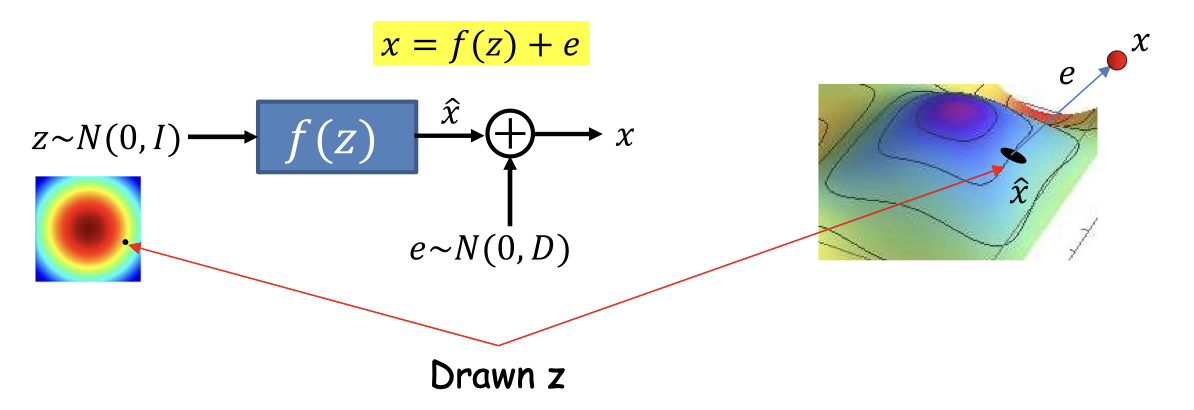
• $f(z)$ is a non-linear function that produces a curved manifold
  • Like the decoder of a non-linear AE
• Generating process
  • Draw a sample $z$ from a Uniform Gaussian
  • Transform $z$ by $f(z)$
    • This places $z$ on the curved manifold
  • Add uncorrelated Gaussian noise to get the final observation

• Key requirement
  • Identifying the dimensionality $K$ of the curved manifold
  • Having a function that can transform the (linear) $K$-dimensional input space (space of $z$ ) to the desired $K$-dimensional manifold in the data space

With complete data

$x=f(z ; \theta)+e$

$P(x \mid z)=N(f(z ; \theta), D)$

• Given complete information $X=\left[x_{1}, x_{2}, \ldots\right], \quad Z=\left[z_{1}, z_{2}, \ldots\right]$

$\theta^{\star}, D^{\star}=\underset{\theta, D}{\operatorname{argmax}} \sum_{(x, z)} \log P(x, z)=\underset{\theta, D}{\operatorname{argmax}} \sum_{(x, z)} \log P(x \mid z)$

$=\underset{\theta, D}{\operatorname{argmax}} \sum_{(x, Z)} \log \frac{1}{\sqrt{(2 \pi)^{d}|D|}} \exp \left(-0.5(x-f(z ; \theta))^{T} D^{-1}(x-f(z ; \theta))\right)$

$=\underset{\theta, D}{\operatorname{argmax}} \sum_{(x, Z)}-\frac{1}{2} \log |D|-0.5(x-f(z ; \theta))^{T} D^{-1}(x-f(z ; \theta))$

• There isn’t a nice closed form solution, but we could learn the parameters using backpropagation

Incomplete data

• The posterior probability is given by

$P(z \mid x)=\frac{P(x \mid z) P(z)}{P(x)}$

• The denominator

$P(x)=\int_{-\infty}^{\infty} N(x ; f(z ; \theta), D) N(z ; 0, D) d z$

• Can not have a closed form solution
  • Try to approximate it

• We approximate $P(z|x)$ as

$P(z \mid x) \approx Q(z, x)=\operatorname{Gaussian} N(z ; \mu(x), \Sigma(x))$

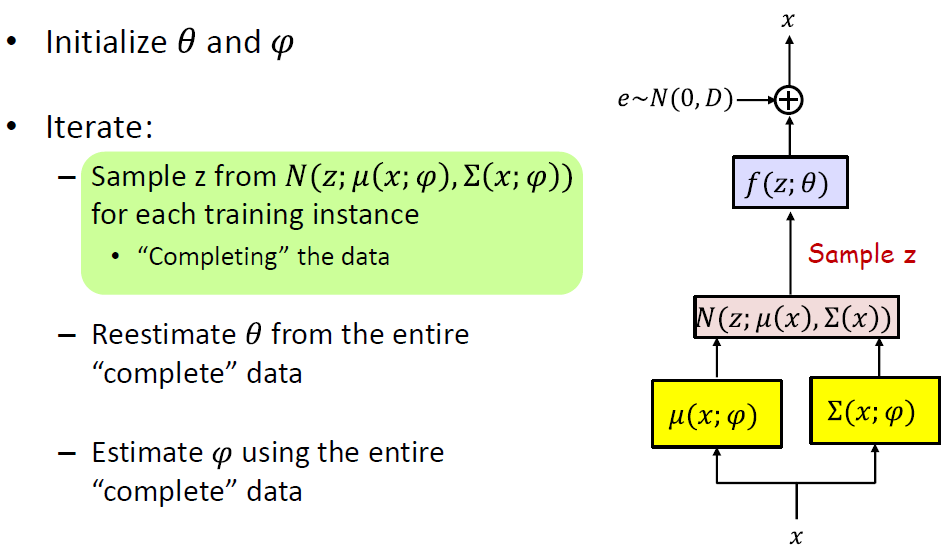
• Sample $z$ from $N(z;\mu (x;\phi),\sigma (x;\phi))$ for each training instance
  • Draw $K$-dimensional vector $\varepsilon$ from $N(0,I)$
  • Compute $z=\mu(x ; \varphi)+\Sigma(x ; \varphi)^{0.5} \varepsilon$
• Reestimate $\theta$ from the entire “complete” data
  • Using backpropagation

$L(\theta, D)=\sum_{(x, z)} \log |D|+(x-f(z ; \theta))^{T} D^{-1}(x-f(z ; \theta))$

$\theta^{\star}, D^{\star}=\underset{\theta, D}{\operatorname{argmin}} L(\theta, D)$

• Estimate $\varphi$ using the entire “complete” data
  • Recall $Q(z, x)=N(z ; \mu(x ; \varphi), \Sigma(x ; \varphi))$ must approximate $P(z|x)$ as closely as possible
  • Define a divergence between $Q(z,x)$ and $P(z|x)$

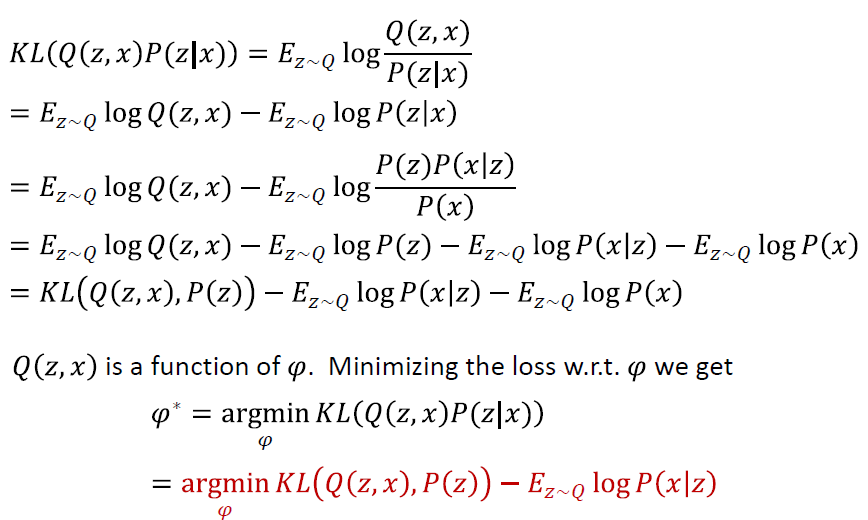
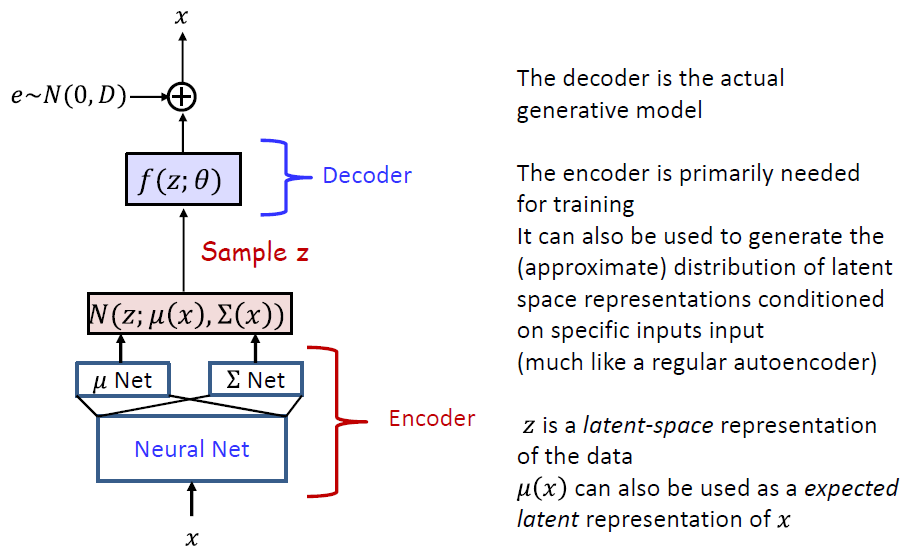
Variational AutoEncoder

• Non-linear extensions of linear Gaussian models
• $f(z;\theta)$ is generally modelled by a neural network
• $\mu(x ; \varphi)$ and $\Sigma(x ; \varphi)$ are generally modelled by a common network with two outputs

• However, VAE can not be used to compute the likelihoood of data
  • $P(x;\theta)$ is intractable
• Latent space
  • The latent space $z$ often captures underlying structure in the data $x$ in a smooth manner
  • Varying $z$ continuously in different directions can result in plausible variations in the drawn output